Turing Machines and Computability

What are the limits (if any) of computers?

To answer this question, we need to clarify the notions of computer and computation

A good theory should be as simple as possible, but not simpler.
—Albert Einstein

A computation is any process that can be described by a set of unambiguous instructions.

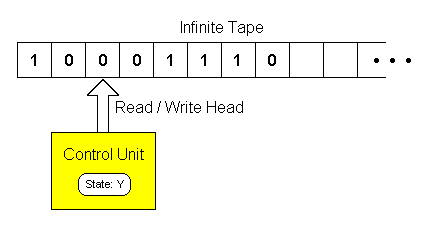
Alan Turing invented the idea of a Turing Machine in 1935-36 to describe computations.

• a Turing Machine is a purely theoretical device
• control unit can be in one of a finite number of states
• each tape cell holds one of a finite number of symbols
• read/write head overwrites current symbol on each step
• read/write head moves one square to the left or right on each step

Example: Inversion

Start State: 1
Halt State: 2

This Turing machine can be viewed as a function that takes an input string and returns the corresponding inverted string (all 1's replaced by 0's and vice versa).

1100  -->  0011
01  -->  10

Turing machine description:

1 0 1 1 R
1 1 1 0 R
1 b 2 b R

Turing Machine Simulator from The Analytical Engine

Is this really enough to compute everything?

Consider:

• Memory is not a problem (tape is infinite)

• Efficiency is not a problem (purely theoretical question)

• Data representation is not a problem (we can use binary, or whatever symbols we like)

• All attempts to characterize computation have turned out to be equivalent

  • Turing machines (Turing)
  • Partial recursive functions (Gödel, Kleene)
  • Lambda calculus (Church)
  • Post production systems (Post)
  • Unlimited register machines (Cutland)
  • Random access machines (Cook and Reckhow)

Church-Turing Thesis Anything that can be computed can be computed by a Turing machine

Choice of programming language doesn't really matter — all are "Turing equivalent"

When we talk about Turing machines, we're really talking about computer programs in general.

Corollary If the human mind is really a kind of computer, it must be equivalent in power to a Turing machine

The Halting Problem

Is there anything a Turing machine cannot do, even in principle?   YES!

No Turing machine can infallibly tell in advance if another Turing machine will get stuck in an infinite loop on some given input.

Example: Looper TM eventually halts on input 0000bbb... but gets stuck in an infinite loop on input 0000111bbb...

Equivalently, no computer program can infallibly tell if another computer program will get stuck in an infinite loop. In other words, no computer program can infallibly tell if another program is completely free of bugs.

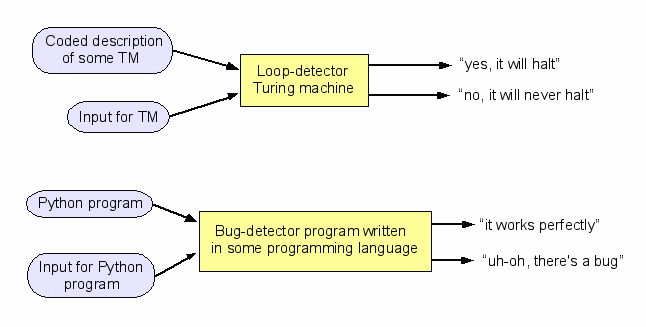
How did Turing prove that such a program is in principle impossible?

We'll use Python instead of Turing machines to illustrate the argument, but the argument is valid no matter what language we use to describe computations (Python, Turing machines, Java, BASIC, etc.)

Turing's approach was to assume that a loop-detector program could be written. He then showed that this leads directly to a logical contradiction!

So, following in Turing's steps, let's just assume that it's possible to write a Python program that correctly tells whether other Python programs will eventually halt when given particular inputs. Let's call our hypothetical program halts. Here's a rough sketch of what it would look like:

def halts(program, data):

   ... lots of complicated code ...

   if ... some condition ...:
      return True
   else:
      return False

Halts takes two inputs, called program and data. The first input is an arbitrary Python program, and the second input represents the data to feed to that program as input. Halts returns either True or False, depending on whether program ever halts when given data as input. For example, let's write a couple of simple Python programs to test halts with:

def progA(input):
  print 'done'

def progB(input):
  if input == 1:
    while True:
      pass         # this causes an infinite loop
  else:
    print 'done'

Now we can ask halts what these programs do when given various inputs. ProgA always halts, no matter what input we give it:

• halts(progA, 1) would return True
• halts(progA, 2) would return True

ProgB loops forever if we happen to feed it the value 1. Any other value will cause it to halt:

• halts(progB, 1) would return False
• halts(progB, 2) would return True

So far, we have every reason to believe that halts could exist, at least in principle, even though it might be a rather complicated program to write. At this point, Turing says "OH YEAH? If halts exists, then I can define the following program called turing which accepts any Python program as input..."

def turing(program):
  if halts(program, program) == True:
    while True:
      pass
  else:
    print 'done'

At this point, we say "Yes, so what?" Turing laughs and says "Well, what happens when I feed the turing program to itself?"

turing(turing)

What happens indeed? Let's analyze the situation:

• The turing program uses halts to analyze the Python program given to it as input:

  • If the Python program halts when fed itself as input, then turing never halts.
  • If the Python program never halts when fed itself as input, then turing prints 'done' and halts.

• But if the Python program happens to be the turing program itself, then:

  • If turing halts when fed itself as input, then turing never halts.
  • If turing never halts when fed itself as input, then turing prints 'done' and halts.

• This is a blatant logical contradiction!

• turing(turing) can neither halt nor loop forever; it doesn't make sense either way.

Thus our original assumption about the existence of halts must have been invalid, since as we just saw, it's easy to define the logically-impossible turing program if halts is available to us.

Q.E.D.

Conclusion The task of deciding if an arbitrary computation will ever terminate cannot be described computationally

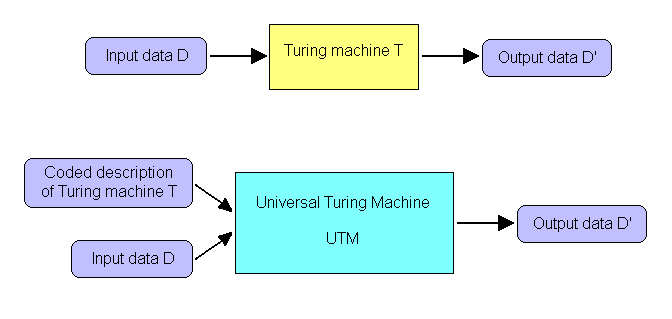
• The UTM accepts a coded description of a Turing machine and simulates the behavior of the machine on the input data.

• The coded description acts as a program that the UTM executes.

• The UTM's own internal program is fixed.

• The existence of the UTM is what makes computers fundamentally different from other machines such as telephones, CD players, VCRs, refrigerators, toaster-ovens, or cars.

• Computers are the only machines that can simulate any other machine to an arbitrary degree of accuracy.
  Example: a calculator simulator written in JavaScript

How can we "encode" a Turing machine?   Here's one way:

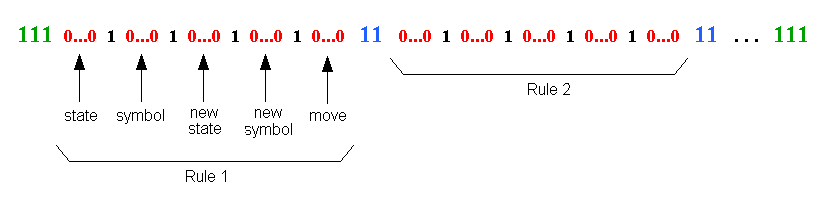
Example: Looper TM

States:  A, B  --> 0, 00
Symbols:  0, 1, b  -->  0, 00, 000
Moves:  Left, Right  -->  0, 00

Rule 1:   A 0 A 0 Right   -->  0101010100
Rule 2:   A 1 A 1 Left   -->  01001010010
Rule 3:   A b B b Right   -->  010001001000100

1110101010100110100101001011010001001000100111

We could run our hypothetical Loop-detector Turing machine on the above encoding with the input 0000111:

Eventually the machine would halt with a single 1 as output, meaning an infinite loop was detected:

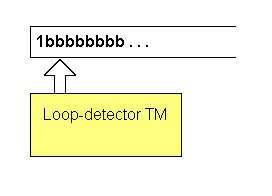
But, alas, we know that such a loop-detecting Turing machine is impossible, as Turing showed.